경마 우승마 예측

순위를 기반으로 한 예측 모형은 경마의 특성상 배팅 방식에 따라 예측해야하는 말의 수가 다르므로 1위인 한 마리를 예측하는 경우, 2위까지 두 마리, 3위까지 세 마리를 예측하는 모형으로 각각 다르게 적합하였다.

예를 들어 n위까지 n마리를 예측하는 모형에서는 순위 값이 1부터 n위인 말의 순위를 1로 바꾸고, 이하 순위의 말은 모두 순위를 0으로 바꾸어 2-class 분류 문제로 변환하여 분석하였다. 순위는 한 경기 내에서 결정되는 값이므로 같은 경주를 뛰는 경주마 간에 차이가 없는 주로 습도 변수는 제외하고 분석하였다.

분류분석방법으로 모든 변수를 전부 이용한 로지스틱 회귀와 AIC, BIC 기준으로 변수선택법 (Park 등, 2011; Venables와 Ripley, 2002)을 이용한 로지스틱 회귀, 그리고 랜덤 포레스트 방법을 이용하여 test data에서의 예측률을 비교하였다.

위의 방법으로 순위를 0, 1로 바꾸면 1보다 0이 훨씬 많은 불균형 데이터이므로 적합시킨 분류 모형으로 test data를 분류하면 각 경기마다 원하는 마릿수만큼 예측이 되지 않는 경우가 있다. 예를 들어, 어느 경기에는 1등 말이 하나도 없는 경우가 나올 수도 있다.

따라서 경기 별로 배팅 방식에 따른 마릿수를 예측하기 위하여 개별 말이 1로 분류 될 예측 확률을 계산하였다. 이후 n마리의 우승마를 예측하기 위해서 각 경기 내에서 1로 분류될 예측 확률이 높은 순서대로 n위까지의 말을 우승마로 하여 1로 나머지를 0으로 분류하였다.

먼저 로지스틱 회귀 모형에 대해서 살펴보면, BIC 기준 로지스틱 모형에서 선택된 변수는 모두 AIC 기준에서 선택된 변수에 포함된다. 그러므로 AIC 기준의 로지스틱 모형에서 선택된 변수 중 유의 수준 0.01하에서 유의한 변수의 부호만을 살펴보았으며 이는 Table 3.1과 같다.

Table 3.1. The important variables of each logistic model

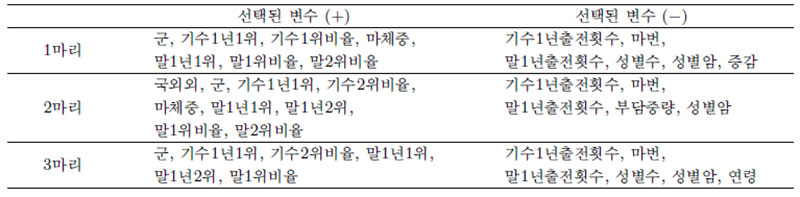
Table 3.2. The important variables of each random forest model

로지스틱 회귀에서 회귀계수가 양수이면 설명변수의 값이 커질수록 우승마가 될 확률이 증가하는 변수임을 의미한다. 양의 효과를 갖는 변수를 살펴보면, 마체중이 무거울수록, 기수와 말의 우승 비율이 높을수록 우승마일 확률이 높아지는 것을 확인할 수 있다.

음의 효과를 갖는 변수를 살펴보면, 마번이 커질수록 우승확률이 낮아지므로 마번이 작은, 즉 안쪽에서 출발하는 것이 유리하다는 사실을 확인할 수 있다. 말의 성별이 수나 암이면 우승할 확률이 작아지며, 회귀계수를 통해 거세마, 수말, 암말 순으로 빠르다는 것을 알 수 있다.

다음은 랜덤 포레스트에 대해서 살펴보고자 한다. 랜덤 포레스트 모형의 경우 로지스틱 회귀에서와 달리 회귀계수의 값이 주어지지 않으므로 변수 중요도가 높은 상위 10개 변수를 살펴보았으며, 이는 Table 3.2에서 확인할 수 있다.

\Table 3.3. Average prediction accuracy in test data.

Table 3.4. The important variables of each linear model

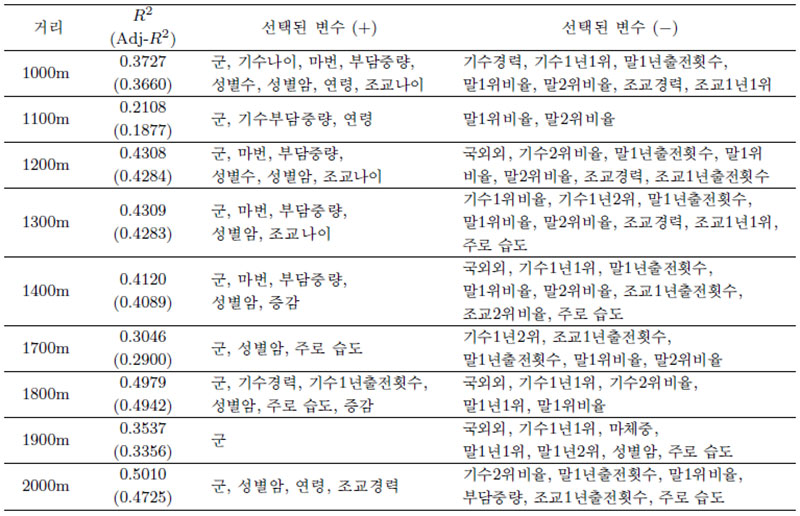
로지스틱 회귀 모형에서와 유사하게 말의 과거 우승 비율, 기수의 우승 비율, 마체중 등이 중요한 변수로 선택된 것을 알 수 있다. 각 모형에 대한 test data에서의 평균 예측률(표준편차)을 계산한 결과는 Table 3.3에서와 같다.

1마리, 2마리 예측에서는 AIC-로지스틱 모형이, 3마리 예측 모형에서는 랜덤 포레스트 모형의 예측률이 가장 높았다. 하지만 1, 2마리 예측에서 AIC-로지스틱 모형과 BIC-로지스틱 모형의 예측력이 거의 같고, 3마리 예측에서는 BIC-로지스틱 모형이 더 우수하였다.

즉, BIC-로지스틱 모형이 AIC-로지스틱 모형 보다 더 간단하고 예측력은 거의 차이가 없으므로 BIC-로지스틱 모형을 최적 모형으로 선택하였다.

그러나 실제 배당률을 적용하여 시행하는 경우에는 어떤 모형이 더 좋은 결과를 나타낼지 알 수 없으므로 3.3절에서 AIC-로지스틱 모형과 BIC-로지스틱 모형을 모두 비교해보고자 한다. 랜덤 포레스트의 최적 모형은 100번 적합 시 train data에서의 예측률을 최대로 하는 모형으로 하였다.